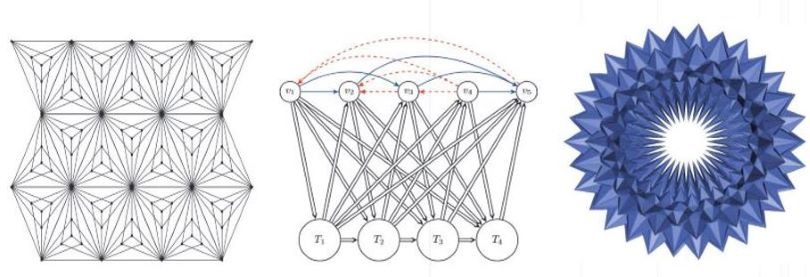
La combinatoire s'est forgée ses propres méthodes qui peuvent aussi faire appel à des outils avancés des mathématiques classiques. De nombreux exemples montrent qu'un outil d'algèbre linéaire, ou de théorie des nombres, ou encore un outil géométrique y compris la programmation en nombres entiers, peut débloquer la solution d'un problème difficile. Les preuves construites ainsi sont souvent simples et élégantes, et conduisent, pour certaines à des résultats fondamentaux et algorithmiquement efficaces. Un outil, qui s'est révélé très puissant est basé sur une idée originale : à un objet combinatoire (par exemple des couplages, des parcours de voyageurs ou des tournées de véhicules), on peut associer un vecteur - souvent le vecteur naturel « d'incidence » de l'objet. Optimiser sur les objets voulus revient à optimiser sur leur enveloppe convexe par des propriétés de base de la programmation linéaire. Ceci est l'idée de départ de la Combinatoire Polyédrale.
 |  |  |
En revanche les contraintes de cette enveloppe convexe ne sont pas nécessairement faciles à déterminer. Cela constitue un sujet de recherches théoriques et appliquées important, conduisant souvent à des problèmes linéaires en nombres entiers. L'équipe contribue à ces recherches, par exemple par l'étude des cônes hilbertiens, des nombres de Carathéodory, ou encore par l'étude d'une conjecture de Berge et Linial sur la couverture des sommets d'un graphe par des cycles. Ces travaux amènent parfois au développement d'algorithmes branch and cut pour la détermination de solutions optimales. Récemment ils ont conduit à un nouvel élan concernant les problèmes de « bin packing », « cutting stock » ou « multiprocessor scheduling ». Pour avancer dans certains travaux, l'utilisation d'autres méthodes géométriques s'est montrée indispensable. Par exemple, les « noyaux » dans les graphes conduisent à des résultats topologiques de Scarf, en lien aussi avec la théorie des jeux. Les « clutters binaires », une généralisation abstraite des « espaces de circuits » des graphes, ont permis de résoudre une grande variété de problèmes (concernant les tournées de postiers, les multiflots, ...) et d'avancer sur le problème de « paintshop scheduling », problème d'ordonnancement de production de l'industrie automobile qui consiste à optimiser la séquence de peinture d'une série de voitures. Récemment nous avons découvert des liens profonds de ce problème avec la topologie combinatoire et la géométrie des polyèdres. Ce lien a permis de mieux cerner la complexité du problème, qui n'entre pas dans les schémas habituels. Cette connexion avec la topologie et la géométrie convexe a déclenché des études approfondies en topologie, et géométrie.